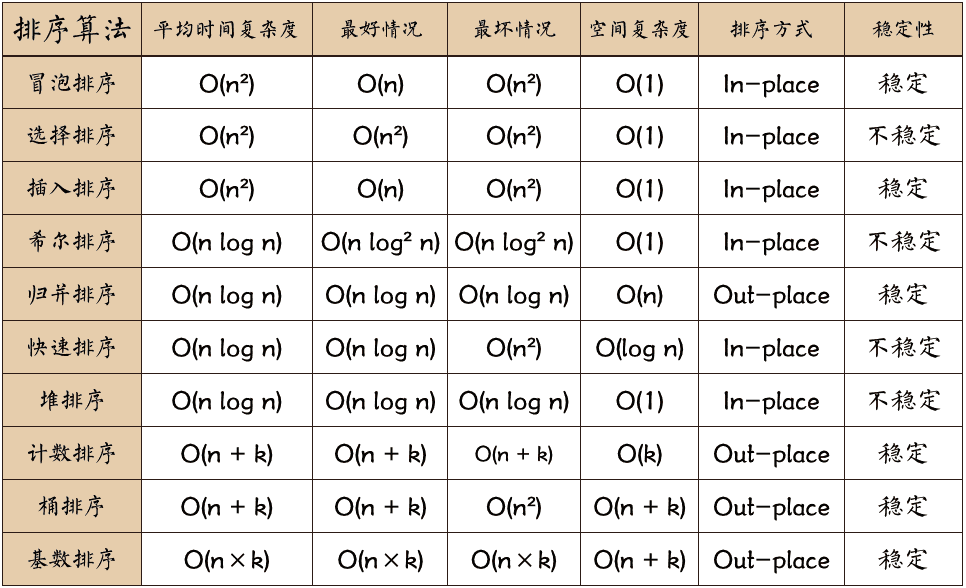
排序算法

希尔排序

希尔排序是基于插入排序的以下两点性质而提出改进方法的，每次取出 gap 间隔的子数组进行插入排序，直到 gap = 1

例如数组：[61, 109, 149, 111, 34, 2, 24, 119, 122, 27]

1. gap = size / 2 = 5：小数组为 [61, 2]、[109, 24]、[149, 119]、[111, 122]、[34, 27]。对小数组进行插入排序：[2, 61]、[24, 109]、[119, 149]、[111, 122]、[27, 34]，结果为：[2, 24, 119, 111, 27, 61, 109, 149, 122, 34]。
2. gap = gap / 2 = 2：小数组为 [2, 119, 27, 109, 122]、[24, 111, 61, 149, 34]，排序后：[2, 27, 109, 119, 122]、[24, 34, 61, 111, 149]，结果为：[2, 24, 27, 34, 109, 61, 119, 111, 122, 149]
3. gap = 1：直接插入排序

void shellsort(int arr[], int n) {
    int gap, i, j, temp;

    for(gap = n/2; gap > 0; gap /= 2){
   		for(i = gap; i < n; i++){
   			for(j = i - gap; j >= 0 && arr[j] > arr[j+gap]; j -= gap) {
                temp = arr[j];
                arr[j] = arr[j+gap];
                arr[j+gap] = temp;
            }
   		}    
    }
}

归并排序

/* 合并左子数组和右子数组 */
void merge(int[] nums, int left, int mid, int right) {
    // 左子数组区间为 [left, mid], 右子数组区间为 [mid+1, right]
    // 创建一个临时数组 tmp ，用于存放合并后的结果
    int[] tmp = new int[right - left + 1];
    // 初始化左子数组和右子数组的起始索引
    int i = left, j = mid + 1, k = 0;
    // 当左右子数组都还有元素时，进行比较并将较小的元素复制到临时数组中
    while (i <= mid && j <= right) {
        if (nums[i] <= nums[j])
            tmp[k++] = nums[i++];
        else
            tmp[k++] = nums[j++];
    }
    // 将左子数组和右子数组的剩余元素复制到临时数组中
    while (i <= mid) {
        tmp[k++] = nums[i++];
    }
    while (j <= right) {
        tmp[k++] = nums[j++];
    }
    // 将临时数组 tmp 中的元素复制回原数组 nums 的对应区间
    for (k = 0; k < tmp.length; k++) {
        nums[left + k] = tmp[k];
    }
}

/* 归并排序 */
void mergeSort(int[] nums, int left, int right) {
    // 终止条件
    if (left >= right)
        return; // 当子数组长度为 1 时终止递归
    // 划分阶段
    int mid = left + (right - left) / 2; // 计算中点
    mergeSort(nums, left, mid); // 递归左子数组
    mergeSort(nums, mid + 1, right); // 递归右子数组
    // 合并阶段
    merge(nums, left, mid, right);
}

快速排序

/* 快速排序 */
void quickSort(int[] nums, int left, int right) {
    // 子数组长度为 1 时终止递归
    if (left >= right)
        return;
    // 哨兵划分
    int pivot = partition(nums, left, right);
    // 递归左子数组、右子数组
    quickSort(nums, left, pivot - 1);
    quickSort(nums, pivot + 1, right);
}

/* 哨兵划分 */
int partition(int[] nums, int left, int right) {
    // 以 nums[left] 为基准数
    int i = left, j = right;
    while (i < j) {
        while (i < j && nums[j] >= nums[left])
            j--;          // 从右向左找首个小于基准数的元素
        while (i < j && nums[i] <= nums[left])
            i++;          // 从左向右找首个大于基准数的元素
        swap(nums, i, j); // 交换这两个元素
    }
    swap(nums, i, left);  // 将基准数交换至两子数组的分界线
    return i;             // 返回基准数的索引
}

void swap(int[] nums, int i, int j) {
    int tmp = nums[i];
    nums[i] = nums[j];
    nums[j] = tmp;
}

最坏情况下：如果数组已经是有序的或逆序的，则每次选取的枢轴都无法有效分割数组。比如对一个已经升序排列的数组进行快速排序：[1,2,3,4,5]，递归树是一个斜树，需要 n - 1 次递归，因此最坏时间复杂度为 O(n^2);

堆排序

算法步骤：

1. 创建一个堆 H[0……n-1]；
2. 把堆首（最大值）和堆尾互换；
3. 把堆的尺寸缩小 1，并调用 shift_down(0)，目的是把新的数组顶端数据调整到相应位置；
4. 重复步骤 2，直到堆的尺寸为 1。

public class HeapSort implements IArraySort {

    @Override
    public int[] sort(int[] sourceArray) throws Exception {
        // 对 arr 进行拷贝，不改变参数内容
        int[] arr = Arrays.copyOf(sourceArray, sourceArray.length);

        int len = arr.length;

        buildMaxHeap(arr, len);

        for (int i = len - 1; i > 0; i--) {
            swap(arr, 0, i);
            len--;
            heapify(arr, 0, len);
        }
        return arr;
    }

    private void buildMaxHeap(int[] arr, int len) {
        for (int i = (int) Math.floor(len / 2); i >= 0; i--) {
            heapify(arr, i, len);
        }
    }

    private void heapify(int[] arr, int i, int len) {
        int left = 2 * i + 1;
        int right = 2 * i + 2;
        int largest = i;

        if (left < len && arr[left] > arr[largest]) {
            largest = left;
        }

        if (right < len && arr[right] > arr[largest]) {
            largest = right;
        }

        if (largest != i) {
            swap(arr, i, largest);
            heapify(arr, largest, len);
        }
    }

    private void swap(int[] arr, int i, int j) {
        int temp = arr[i];
        arr[i] = arr[j];
        arr[j] = temp;
    }
}