Morii

Appearance

二叉树 ​

理论 ​

分类 ​

  1. 满二叉树：每一层节点都满(2^(h-1))
  2. 完全二叉树：除最底层都满，最底层集中在左侧
  3. 二叉搜索树：有序树，左子树 < 根节点 < 右子树
  4. 平衡二叉搜索树：AVL 树，空树/左右两个子树高度差不超过 1

遍历方式 ​

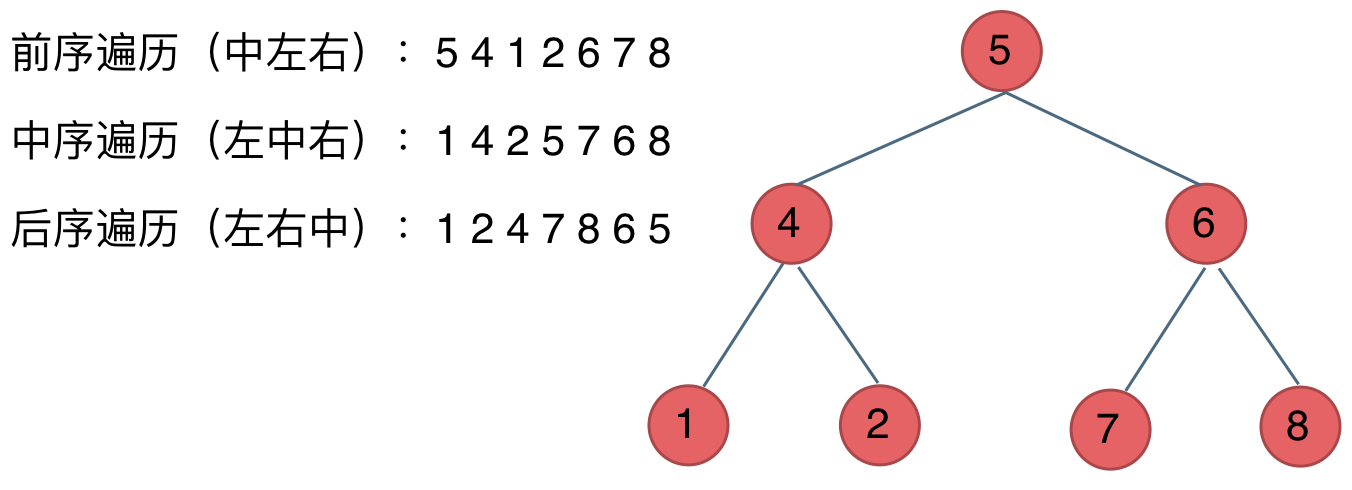
20200806191109896
  1. 前序遍历：根结点 ---> 左子树 ---> 右子树
  2. 中序遍历：左子树 ---> 根结点 ---> 右子树
  3. 后序遍历：左子树 ---> 右子树 ---> 根结点
  4. 层次遍历：只需按层次遍历即可

二叉树遍历 ​

递归遍历 ​

java
class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> result = new ArrayList<Integer>();
        preorder(root, result);
        return result;
    }

    public void preorder(TreeNode root, List<Integer> result) {
        if (root == null) {
            return;
        }
        result.add(root.val);				// 前序遍历位置
        preorder(root.left, result);
        preorder(root.right, result);
    }
}

迭代遍历 ​

使用栈来模拟递归，对于要输出的节点，使用 null 来标记

例如：前序遍历顺序为 中 -> 左 -> 右，入栈顺序为 右 -> 左 -> 中，而中节点要输出，则 push 一个 null 节点，下次遇到 null 节点则取出栈首元素加入结果集

java
class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> result = new LinkedList<>();
        Stack<TreeNode> st = new Stack<>();
        if (root != null)
            st.push(root);
        while (!st.empty()) {
            TreeNode node = st.peek();
            if (node != null) {
                st.pop(); // 将该节点弹出，避免重复操作，下面再将右中左节点添加到栈中
                if (node.right!=null) st.push(node.right);  // 添加右节点（空节点不入栈）
                if (node.left!=null) st.push(node.left);    // 添加左节点（空节点不入栈）
                st.push(node);                          // 添加中节点
                st.push(null); // 中节点访问过，但是还没有处理，加入空节点做为标记。           
            } else { // 只有遇到空节点的时候，才将下一个节点放进结果集
                st.pop();           // 将空节点弹出
                node = st.peek();    // 重新取出栈中元素
                st.pop();
                result.add(node.val); // 加入到结果集
            }
        }
        return result;
    }
}

层次遍历 ​

迭代方式 - 队列 - BFS

java
class Solution {
    public List<List<Integer>> levelOrder(TreeNode root) {
        List<List<Integer>> res = new ArrayList<>();
        if(root == null)
            return res;
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);

        while(!queue.isEmpty()){
            List<Integer> list = new ArrayList<>();

            int len =  queue.size();
            
            while(len > 0){
                TreeNode temp = queue.poll();
                list.add(temp.val);

                if(temp.left != null)
                    queue.offer(temp.left);
                if(temp.right != null)
                    queue.offer(temp.right);
                len--;
            }
            res.add(list);
        }
        return res;
    }
}

递归方式

java
class Solution {
    public List<List<Integer>> resList = new ArrayList<List<Integer>>();
    
    public List<List<Integer>> levelOrder(TreeNode root) {   
        checkFun01(root,0);
        return resList;
    }
    
    //DFS--递归方式
    public void checkFun01(TreeNode node, Integer deep) {
        if (node == null) return;
        deep++;

        if (resList.size() < deep) {
            //当层级增加时，list的Item也增加，利用list的索引值进行层级界定
            List<Integer> item = new ArrayList<Integer>();
            resList.add(item);
        }
        resList.get(deep - 1).add(node.val);

        checkFun01(node.left, deep);
        checkFun01(node.right, deep);
    }
}

多叉树遍历 ​

java
/*
// Definition for a Node.
class Node {
    public int val;
    public List<Node> children;

    public Node() {}

    public Node(int _val) {
        val = _val;
    }

    public Node(int _val, List<Node> _children) {
        val = _val;
        children = _children;
    }
};
*/

class Solution {
    List<Integer> res = new ArrayList<>();
    
    public List<Integer> preorder(Node root) {
        pre(root);
        return res;
    }

    public void pre(Node root){
        if(root == null)
            return;
        
        res.add(root.val);		// 前序遍历
        for(int i = 0;i < root.children.size();i++){
            pre(root.children.get(i));
        }
    }
}